Boole cebri. Bölüm 2. Temel kanunlar ve fonksiyonlar

Boole cebri, konvansiyonlar, kurallar, işlemler hakkındaki hikayenin devamı. Kontak devrelerinin temellerine geçiş.

ilk makale George Bull, mantık cebirinin yaratıcısı olarak tanımlandı. İkinci makale Boole cebirinin temel işlemlerini ve Boole ifadelerini basitleştirme yöntemlerini açıklayacaktır. Dolayısıyla, Boole cebiri ifadeleri argüman olarak kullanır, anlamlarını değil, ifadenin gerçekliğini veya sahtelikini kullanır.

Boole cebrinde ifade yazma formu.

İfade doğruysa, şu şekilde yazılır: A = 1, yanlışsa, A = 0 (patatesin bir meyve olduğu doğru değildir). Herhangi bir ifade için A, true (A = 1) veya false (A = 0) şeklindedir. Burada orta yok. Bunu zaten konuşmuştuk.

Birliğe iki basit ifade bağlarsanız Ve mantıksal ürün olarak adlandırılan karmaşık bir ifade alırsınız. İki basit söz alalım: “Üç ikiden fazla” A harfiyle, “Beşten az üç” - B harfiyle atayacağız.

Bu nedenle, “Üç ikiden fazla ve beşten az” diyen karmaşık mantıklıdır (bu durumda, büyük harf I, bunun “VE” ve “DEĞİL” metninde olduğu gibi “VE” mantıksal bir işlem olduğunu belirtir). ve B. Aşağıdaki gibi tanımlanmıştır: A ^ B veya A * B.

Mantıksal çarpma (işlem "VE").

Temel cebirde A * A = A2. Ama Buhl’un cebirinde A * A = A2 = A, A * A = A, çarpma işareti (*) artık ... Ve ... And anlamında ... Ve. Tüm deneyimlerimiz A&A'nın sadece A. ile aynı olduğunu teyit eder. İfadenin gerçeği, faktör tarafından birkaç kez tekrarlanırsa değişmez.

Bu durumda iki ifadenin çarpımı doğru (1'e eşit) ve yalnızca her iki faktör de doğruysa ve yanlış (0'a eşit) olarak kabul edilir. Bu kuralların sağduyu ile çelişmediğini ve ayrıca temel cebir kurallarına tam olarak uyduklarını kabul edin:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

İlk eşitlik şu şekildedir: A ve B'nin ikisi de doğruysa, A * B ürünü doğrudur. Buhl cebirinde çarpma işareti (*) I birleşiminin yerini alır.

Mantıksal ürünler iki değil, daha fazla sayıda ifade - faktör içerebilir. Ve bu durumda, ürün sadece aynı zamanda tüm ifade faktörleri doğru olduğunda doğrudur.

Mantıksal toplama (VEYA işlemi)

İki ifade bir sendika ile bağlıysa VEYA. oluşan bileşik cümleye mantıksal toplam denir.

Mantıksal bir toplam örneği düşünün. A diyerek: "Bugün sinemaya gideceğim."

Açıklama B: “Bugün diskoya gideceğim.” Her iki ifadeyi de ekliyoruz: "Bugün filmlere VEYA bir diskoya gideceğim."

Bu karmaşık ifade şu şekilde ifade edilir: A + B = C veya (A V B) = C.

C ile mantıksal bir toplamın karmaşık bir ifadesini gösterdik.

Söz konusu örnekte, VEYA birliği münhasır anlamda kullanılamaz. Gerçekten de aynı gün sinemaya ve diskoya gidebilirsiniz. Ve işte deyiş:

“Bahçecilik ortaklığının başkanı Petrov veya Ivanov olacak” - mantıklı bir toplam değil, çünkü sadece bir kişi başkan olacak ve diğeri amatör sıradan bir bahçıvan olacak.

Mantıksal toplam için V işareti, "ve" anlamına gelen Latince "aut> kelimesinin aksine" vel "kelimesinin ilk harfi olduğu için seçilir. Şimdi, herkesin mantıklı ürünün neden ^ işareti ile belirtildiği açık olmalıdır.

Temel cebirde A + A = 2A kuralı vardır. Bu kural doğrudur, hangi sayı A harfi ile temsil edilirse gösterilsin, Boolean cebirinde A + A = A kuralı buna karşılık gelir.Tüm yaşam deneyimimiz, A OR A veya her ikisinin de A'yı sadece A demenin başka ve daha uzun bir yolu olduğunu söyler.

Herhangi bir bileşik ifadesi gibi, iki A ve B ifadesinin toplamı doğru veya yanlış olabilir. Eğer terimlerden en az biri doğruysa, toplam doğru, yani birliğe eşit olarak kabul edilir:

Geleneksel aritmetik ile tutarlı olan VEYA A = 1 VEYA B = 1 ise A + B = 1:

1+0 = 0+1 = 1.

Her iki toplanan ifade de doğruysa, toplam da doğru olarak kabul edilir, bu nedenle Boole cebrinde: (1) + (1) = 1 vardır.

Köşeli ayraçlar, aritmetik değil, bu eklemenin koşulunu, anlamını vurgulamak için burada ayarlanır.

İki ifadenin toplamı yanlış ve sıfıra eşit olarak kabul edilir, ancak yalnızca her iki terim de yanlışsa. Buradan:

0 + 0=0.

Dolayısıyla, A + B ifadelerinin toplamı doğru ise doğru kabul edilir, VEYA A, OR B, VEYA her iki terim birlikte. Böylece, OR kelimesi + ile gösterilir.

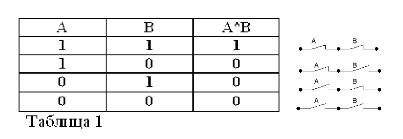
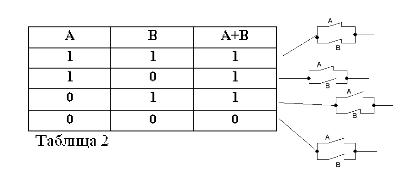
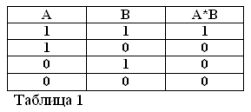
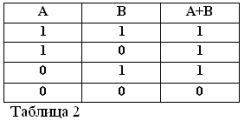
A ve B ifadelerinin sadece doğru veya yanlış olabileceğini ve bu nedenle 1 veya 0 doğruluk ölçüsüne sahip olabileceğini hatırlayarak, dikkate alınan AND ve OR işlemlerinin sonuçları tablo 1 ve 2'de özetlenebilir.

Buhl cebiri tarafından yaygın olarak kullanılan üçüncü işlem, olumsuzlama işlemidir - DEĞİL. Temel cebirin ADD, D Çıkarma, Çarpma, Bölme ve diğer işlemlerini kullandığını hatırlatırız.

Her A ifadesi için, / A sembolü ile göstereceğimiz, A DEĞİL olumsuzlaması vardır. Bu şüpheye düşmemelidir.

Örnekler veriyoruz: “Ormana gideceğiz” A, “Ormana gitmeyeceğiz” / A.

A ifadesi doğruysa, yani, A = 1 ise, olumsuzluğu / A yanlış / A = 0 olmalıdır. Tersi, eğer herhangi bir ifade yanlışsa, olumsuzlaması doğrudur. Örneğin: “At saman yemez” / A = 0, “At saman yemez” (A = 1). Bu tablo 3'te ifade edilebilir.

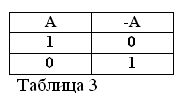
Olumsuzluk eyleminin anlamını belirlemek ve iki A ve / A ifadesinin her zaman doğru olduğunu varsayarsak, Boole cebirinin iki yeni formülü aşağıdaki gibidir:

A + (/ A) = 1 ve A * (/ A) = 0.

İfadelerin mantıksal işlenmesini basitleştiren başka formüller de vardır. Örneğin, 1 + A = 1, toplama tanımına göre, bir terimin birliğe eşit olduğu durumda, toplam her zaman birliğe eşittir. Elde edilen sonuç A = 0 veya A = 1 olup olmamasına bağlı değildir.

İncelediğimiz üç mantıksal işlemin her biri (VE, VEYA, DEĞİL), temel cebir kurallarına yakın belirli özelliklere sahiptir. Hepsi formüle edilirse, 25 Boole cebiri kuralı alırız. Hemen hemen her mantıksal sorunu çözmek için yeterlidirler. Bu kurallar olmadan, görünür karmaşıklıkları nedeniyle mantıksal sorunları çözmek oldukça zorlaşır. Kuralları kullanmadan doğru cevabı bulmaya çalışmak, onları yaratıcılık ve genel akıl yürütme ile değiştirmek anlamına gelir. Kurallar bu işi büyük ölçüde kolaylaştırır ve zaman kazandırır.

Makale çerçevesinde, tüm bu 25 kuralı dikkate almak imkansızdır, ancak isteyenler bunları her zaman ilgili literatürde bulabilirler.

1938'deki ilk makalede daha önce de belirtildiği gibi, genç Amerikalı bilim adamı Claude Shannon, “Röle ve Anahtarlama Devrelerinin Sembolik Analizi” makalesinde ilk kez röle teknolojisi problemleri için Boole cebirini kullanıyor. Shannon'ın keşfi, röle makineleri ve elektronik bilgisayarlar tasarlama yönteminin aslında matematiksel mantığın bir dalı olduğunu fark etmesiydi.

Sık sık olur. Uzun yıllardır, bilim adamı yurttaşları için tamamen gereksiz görünen bir sorun üzerinde çalışıyor - sadece eğlence. Ancak onlarca yıl ve bazen yüzyıllar geçiyor ve kimsenin ihtiyaç duymadığı bir teori sadece var olma hakkını elde etmekle kalmıyor, aynı zamanda daha fazla ilerleme düşünülemez hale geliyor.

Shannon'ın ikinci kez Boole cebirini “keşfetmesine” ne yardımcı oldu? dava? Bu tür bir şey yok.

Konvansiyonel anahtarlar ve röleler üzerine inşa edilen röle makinelerinin sevgisi, genç bilim adamının unutulmuş bir teoriyi o sırada üzerinde çalıştığı otomatik telefon santralleri ile ilişkilendirmesine yardımcı oldu. Daha sonra Shannon, aynı “evet ya da hayır” fikrini ayrı mesajlara sundu ve sibernetik - bilgi teorisinin bütün bir bölümünün temelini attı.

Buhl'un cebiri röle devrelerinin analizi ve sentezi için çok uygundur. Gerçek bir ifade olarak kabul etmek yeterliydi: “Devrede bir sinyal var” ve yanlış bir - “Devrede sinyal yok”, yeni bir cebir ortaya çıktıkça - sinyal cebiri, röle devresi cebiri.

Yeni cebir sadece röle ve anahtarlama devrelerinin dikkate alınması için geçerlidir. Sonuçta, sadece bu tür şemalarda “bir sinyal var” ve “sinyal yok” koşulu sağlanmıştır. Sinyalin sürekli olarak değiştiği, keyfi olarak çok sayıda ara koşul (böyle bir sinyale analog denir) edinilmesi durumunda, röle cebiri uygulanamaz. Bu her zaman hatırlanmalıdır. Ancak elektronik bilgisayarların ve sibernetik makinelerin sadece çoğunluğu “evet - hayır” elementlerine dayanan ayrı sinyal işleme prensibini kullanır.

“Kontak kapalı” ifadesi Shannon tarafından true (1) ve “Contact open” yanlış (0) olarak kabul edildi. AND, OR, NOT ve 25 kuralları dahil olmak üzere "cebir" in geri kalanı Shannon, Boole'den ödünç aldı.

Röle devresi cebiri Boolean cebirinden daha basit çıktı, çünkü sadece "evet - hayır" tipi elemanlarla ilgileniyor. Ek olarak, yeni cebir daha görseldir.

Bu cebirdeki elemanlar A, B, C harfleriyle göstereceğimiz kontaklardır. Kontak kapalı - A, kontak açık - / A (kesik harfli).

Gördüğünüz gibi gösterim tamamen Boole cebirinden alınmıştır. Açık bir temas, kapalı bir temasın reddedilmesidir. Aynı kontak hem kapalı hem de açık olamaz.

Herhangi bir devrede iki kontak aynı harfle belirtilirse, bu her zaman aynı değerleri aldıkları anlamına gelir.

Herhangi bir anda, ikisi de aynı anda açık veya ikisi de kapalı. Mekanik olarak birbirine bağlı olduklarını hayal etmenin en kolay yolu, her ikisi de aynı anda açılır veya kapanır.

Bazı zincirlerde herhangi bir temas başka bir temasın olumsuzlamasıysa, anlamları her zaman zıttır. Örneğin, C ve / C kontakları asla aynı anda açık veya aynı anda kapatılamaz. Ve şemada mekanik olarak bağlı olarak temsil edilebilirler: biri açılırsa, diğeri kapanır.

AND, OR ve NOT işlemlerine karşılık gelen en basit devreleri analiz ederek röle cebiri ile tanışmaya başlarız.

İki kontağın ürünü (işlem AND), seri bağlantılarının bir sonucu olarak elde edilen devredir: sadece her iki kontak da kapalı olduğunda (1'e eşit) kapalıdır (1'e eşittir).

İki kontağın (VEYA çalışması) toplamı, paralel bağlandıklarında oluşturulan devre olacaktır: devreyi oluşturan kontaklardan en az biri kapalı olduğunda (1'e eşit) kapalıdır (1'e eşittir).

Bu kontağın tersi (çalışma DEĞİL), bu kontak 1 (kapalı) ise 0 (açık) veya tam tersi bir konudur.

Boolean cebirinde olduğu gibi, kontaklar A ve B harfleriyle gösterilirse, o zaman A * B ile iki kontağın, A + B ile toplamın ve A'nın karşısındaki kontağın / A ile temasını göstereceğiz. Yukarıdakiler Şekil 1, 2 ve 3'te açıklanmaktadır.

AND, OR ve NOT işlemlerine karşılık gelen tabloların geçerliliği. şimdi hiç kimse şüphe etmemeli.

İki örnek üzerinde duralım: 1 * 0 = 0 ve 1 + 0 = 1.

Şekilde görülebildiği gibi, sürekli açık bir kontak ile seri olarak bağlanmış kalıcı olarak kapalı bir kontak, sürekli olarak açık bir kontağa eşdeğerdir (1 * 0 = 0) Sürekli açık bir kontağa paralel olarak bağlanmış, kalıcı olarak kapalı bir kontağın kalıcı olarak kapalı bir kontağa eşdeğer olduğu görülebilir.

Kontak devrelerinin aritmetiği ile tanıştıktan sonra, kabul edilen kuralları kullanarak herhangi bir röle devresini bir formülle tanımlayabilirsiniz. Sibernetikte, bu formüllere yapısal denir.

Herhangi bir röle devresinin yapısal formülü 1 ise, bir sinyal içinden geçebilir - devre kapatılır. Tersine, devrenin yapısal formülü 0 ise, sinyal içinden geçmez - devre kesilir.Sonuç: yapısal formülleri eşit olduğunda iki röle devresi birbirine eşittir.

Makalenin devamında, temas devrelerine, tipik temas devrelerine ve eşdeğerlerine örneklerin yanı sıra yapısal formüllere göre diyagramlar çizeceğiz. Ayrıca Boole cebirinin işlevlerini yerine getiren ana mantık devrelerini de dikkate alıyoruz.

Makalenin devamı: Boole cebri. Bölüm 3. İletişim şemaları

Boris Aladyshkin

Comments

[#1 Alex]

Teşekkür ederim

Sadece bir nokta, paragraf:

"Boolean cebirinde olduğu gibi, kontaklar A ve B harfleriyle gösterilirse, o zaman A * B ile iki kontağın, A + B ile toplamın ve A'nın karşısındaki kontağın / A ile temasını göstereceğiz. Yukarıdakiler Şekil 1, 2 ve 3'te açıklanmaktadır ..."

Şekil 3 nerede?