Boole cebri. Bölüm 1. Biraz tarih

Okulda hepimiz cebir okuduk ama orada Boole cebri hakkında konuşmadılar. Boolean cebiri ile okul cebiri arasındaki fark nedir, görünüşünün tarihi, sorunları ve uygulamaları bu makalede açıklanmıştır.

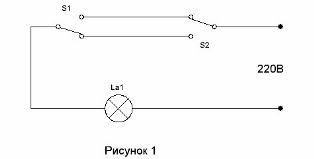
İki anahtarın koridorun girişinde koridordaki ışığı açmasına ve odaya girerken kapanmasına izin veren devre çok uzun süredir bilinmektedir (bkz. Koridor Aydınlatma Kontrol Devresi). Şekil 1'de gösterilmiştir.

Görev numarası 1. Daha karmaşık. 3 farklı anahtardan herhangi biriyle odanızdaki ışığı açıp kapatmanızı sağlayan bir diyagram oluşturun. Anahtarlar odanın girişinde, yatağın üstünde ve masada bulunur.

Görev numarası 2.

Fabrika komitesi gibi bir spor komitesinde 5 hakem toplandı.

Her biri farklı kararlar için oy kullanmak zorundadır. Karar oy çokluğu ile alınır, ancak sadece komite başkanının oyu alması şartıyla.

Hâkimler, oturdukları masanın altında bulunan anahtara basan düğmeye basarak oy kullanırlar. Anahtarı kapatarak, eksilerini keserek lehte oy verirler. Oylama sonuçlarını otomatik olarak görmenizi sağlayan basit bir diyagram çizin. En basit durumda, sadece bir ampul yardımıyla - aydınlandı - karar verildi, yanmadı - hayır.

Görev numarası 3. Uygulamada, bu olası değildir, ancak karmaşık bir eğitim görevi olarak oldukça uygundur.

Büyük bir altıgen odada, her duvara bir anahtar monte edilir. Herhangi bir zamanda bir (herhangi) anahtarı çevirerek odadaki ışığı açabileceğiniz veya kapatabileceğiniz bir devre oluşturun.

Görevleri üç ila dört gün boyunca başarısız bir şekilde yerine getirdikten sonra geçici olarak bir kenara koyun. Ve meşgul ol Boolean cebiri. Boole cebiri ya da aynı zamanda, Boolean cebiri, röle devre cebiri, sorunlarınızı çözmenize yardımcı olacaktır.

Boolean cebiri nedir?

Garip bir şekilde, beş yıldır okulda cebir okuyor olmalarına rağmen, birçok öğrenci ve daha sonra yetişkinler, cebir nedir? Cebir, bazı elementlerin setlerini ve üzerlerindeki eylemleri inceleyen bir bilimdir.

Cebirdeki bir okul kursunda, bu tür unsurlar sayıdır. Rakamlar rakamlarla değil, harflerle belirtilebilir, herkes buna aşinadır. Cebirin ilk derslerinde, bu birçok öğrenci için her zaman zorlaştırır. İlk başta sayılar yerine harf eklemeye alışmanın, hiçbir şey söylemeyen denklemleri çözmenin ne kadar zor olduğunu hatırlayın.

Muhtemelen, her birimiz kendimize şu soruyu sorduk: “Neden rakamlar yerine harfleri girmemiz gerekiyor ve bu hiç gerekli mi?” Ve ancak daha sonra problemleri aritmetiğe kıyasla çözerken cebirin ne gibi avantajlar sağladığını gördünüz.

Cebir birçok tam bilimlerde kullanılır. Bu fizik, mekanik, sopromat, elektrik. Ohm Kanunu bir cebirsel denklemden başka bir şey yoktur: yükte hangi akımın akacağını veya devrenin bir bölümünün hangi dirence sahip olduğunu bulmak için harfler yerine sayısal değerlerini değiştirmek yeterlidir.

Böylece sayı cebiri veya temel cebir ile tanıştınız. Temel ve neredeyse benzersiz görev şu soruyu yanıtlamaktır: “X eşittir? Ne kadar? ”

Lisede, vektör cebirinin başlangıcını incelerler. Bu cebir temel olarak temel cebirden farklıdır. İncelenen kümenin ve diğer eylem kurallarının farklı bir doğası vardır. Vektör denklemini çözerek, cevaba sıradan “Ne kadar?” Sorusunu cevaplayan sıradan bir sayı olmayan bir vektör verilir.

Vektör cebirinin formülleri, birçok açıdan temel cebirin formüllerinden farklıdır. Örneğin, temel cebirde ve vektör cebirde bir ekleme işlemi vardır. Ancak tamamen farklı şekillerde gerçekleştirilir.Sayıların eklenmesi, vektörlerin eklenmesi ile aynı değildir.

Başka cebirler de vardır: doğrusal cebir, yapıların cebiri, halkaların cebiri, mantık cebiri veya aynı şey nedir, Boole cebiri. Muhtemelen okul derslerinde adı duymadınız. George Boole - ama herkes yetenekli kızlarından biri olan Ethel Voinich'in adını biliyor (1864 - 1960). İtalyan karbonarların hakları mücadelesini anlatan "Gadfly" romanını yazdı.

George Bull, 2 Kasım 1815'te İngiltere'de doğdu. Tüm hayatı boyunca okulda matematik ve fizik öğretmeni olarak çalıştı. Öğrencilerinin anılarından Bul'un öğrencilerin yaratıcı yeteneklerinin gelişimine ne kadar büyük önem verdiği bilinmektedir. Yeni materyal sunarken, öğrencilerinin belirli formülleri ve yasaları “yeniden keşfetmelerini” sağlamaya çalıştı.

Öğrencilere, bilim adamlarının kaçınılmaz olarak doğruluk arayışında karşılaştıkları zorlukları anlatan öğretmen, bir Doğu bilgeliğini tekrarlamayı severdi: Farsça taht bile bir kişiye en küçük bilimsel keşif kadar çok zevk getiremez. Buhl, bir gün öğrencilerinin gerçek bir keşif yapma umudunu asla kaybetmedi.

Buhl'un bilimsel ilgi alanları çok genişti: matematik ve mantıkla aynı derecede ilgileniyordu - yasaların bilimi ve düşünme biçimleri. O günlerde mantık bir beşeri bilimler bilimi olarak kabul edildi ve George Boole'yi bilen birçok kişi, matematiğin doğasında olan kesin biliş yöntemlerinin ve tamamen tanımlayıcı mantık yöntemlerinin bir kişide nasıl var olabileceğine şaşırdı.

Ancak bilim adamı, hukuk ve düşünce biçimlerinin bilim ve fizik gibi doğa bilimlerinden herhangi biri kadar katı olmasını istedi. Bunun için, Boule sayıları sıradan cebirde olduğu gibi harf olarak değil, ifadelerde göstermeye başladı ve cebirsellere çok benzeyen bu tür denklemlerin insan tarafından yapılan ifadelerin gerçeği ve sahteliği hakkındaki soruları çözebileceğini gösterdi. Böylece Boole cebri ortaya çıktı.

Ancak Alman matematikçi ve filozof Gottfried Leibniz (1646-1716) George Buhl'dan çok önce, sıradan konuşma dili ile ilgili tüm kavramları sembollerle belirleyecek ve bu sembolleri birleştirmek için yeni bir cebir kuracak bir fikir yarattı.

Böyle bir bilimin yaratılmasından sonra, Leibniz'e göre, bilim adamları ve filozoflar birbirlerini tartışmayı ve bağırmayı, gerçeği bulmayı bırakacaklar, ancak bir kalem alıp sakince şöyle diyecekler: “Hadi hesaplayalım!”

Bugün, mantık cebiri matematiğin önemli bir parçası haline gelmiştir. Görevlerinden biri, sayısal oranları alfabetik olanlarla değiştirilen her türlü denklemi çözmek. Muhtemelen hayatınız boyunca her biriniz, ikinci ve üçüncü derecedeki denklemlerin harf katsayılarıyla nasıl çözüleceğini hatırladınız. Böylece, Boole yeni cebirinde tüm bu formülleri ve kuralları kullandı.

Boole cebirinde yeni olan şey, üzerinde çalışılan kümenin öğelerinin sayı değil, ifadeler olmasıdır. Sıradan cebirsel denklemleri çözerken, bilinmeyen X'in hangi sayıya eşit olduğu belirlenirse, okul cebiri “Ne kadar?” Sorusunun cevabını arar.

Mantık cebiri şu soruya cevap aramaktadır: “X harfi ile gösterilen bu ifade doğru mu?”

İfadenin anlamı ve içeriği burada herhangi bir rol oynamaz. Her ifade yalnızca doğru veya yanlış olabilir. Yarı doğru, yarı yanlış olamaz. Örnek olarak, bir madeni para ile lotları savurmayı hatırlayabiliriz.

Orada sadece iki madeni para durumu kabul edilir - kafalar veya kuyruklar. Tarafların mutabakatı ile, kartal EVET ve kuyruklar HAYIR. Mümkün olmalarına rağmen, olasılık teorisinde başka hiçbir ara nokta dikkate alınmaz. Ters çevrilmiş bir para bir kenara düşebilir, zemini bir sandalyenin veya masanın bacaklarına yuvarlayabilir ve dik bir pozisyonda kalabilir veya hatta zeminde geniş bir boşluğa düşebilir. (Elektrik devrelerine benzer şekilde, son iki durum yanmış kontak şeklinde bir arıza olarak düşünülebilir).Ancak o günlerde, Boole cebiri, ne yazık ki, yaygın olarak kullanılmadı.

Claude Shannon, Bühl cebirini yeniden “keşfetti”. 1938'de, Massachusetts Teknoloji Enstitüsü ve Amerika'da hala bir öğrenci iken, genç Claude Boolean cebirinin röle ve anahtarlama devrelerinin analizi ve sentezi için tamamen uygun olduğunu kanıtladı.

Boolean cebirinin yardımıyla, bir rölede çalışan bir otomatın elektrik devresini yapmak çok kolaydır.Bunun için, sadece makinenin tam olarak ne yapması gerektiğini bilmeniz gerekir, yani çalışması için bir algoritmaya sahip olmanız gerekir. Böylece EVET veya HAYIR prensibi ile çalışan dijital makineler teorisi için temel atılmıştır.

Kısacası, Boole cebirinin tarihi budur. Aşağıdaki makalelerde temel yasalarını, bu yasaları uygulayan temas devresi örneklerini ele alacağız. Makalenin başında verilen görevlerin çözümünü düşünün.

Makalenin devamı: Boole cebri. Bölüm 2. Temel kanunlar ve fonksiyonlar

Boris Aladyshkin