"Her şey akar" ya da meraklılar için Ohm Yasası

10. sınıfta bir süre çalışmış olan son mokasen bile öğretmene Ohm yasası - bu “U, I çarpı R çarpıdır”. Ne yazık ki, en zeki mükemmel öğrenci biraz daha söyleyecek - Ohm yasasının fiziksel tarafı yedi mühür için gizemini koruyacak. Görünüşte bu ilkel konuyu sunma konusundaki deneyimimi meslektaşlarımla paylaşmama izin veriyorum.

Pedagojik faaliyetimin amacı, okurun tahmin ettiği gibi fizikten çok uzak olan sanat ve insancıl 10. sınıftı. Bu nedenle, bu konunun öğretilmesi, genel olarak, biyoloji öğreten bu satırların yazarına emanet edilmiştir. Birkaç yıl önceydi.

Ohm yasası ile ilgili ders, elektrik akımının yüklü parçacıkların bir elektrik alanındaki hareketi olduğu önemsiz ifadesiyle başlar. Yüklü bir parçacık üzerinde sadece bir elektrik kuvveti etki ederse, parçacık Newton’un ikinci yasasına göre hızlanır. Yüklü parçacık üzerine etkiyen elektrik kuvveti vektörü tüm yörüngede sabitse, o zaman eşit olarak hızlanır. Tıpkı bir ağırlığın yerçekimi etkisi altına girmesi gibi.

Ama burada paraşütçü tamamen yanlış düşüyor. Rüzgarı ihmal edersek, düşme oranı sabittir. Sanat ve insani sınıftaki bir öğrenci bile, yerçekimi kuvvetine ek olarak, bir kuvvet daha düşen paraşüt üzerinde hareket eder - hava direncinin gücü. Bu kuvvet, mutlak değerde, paraşütün Dünya tarafından çekim gücüne eşittir ve yönünün tersidir. Neden? Bu dersin kilit sorusudur. Bazı tartışmalardan sonra, çekme kuvvetinin artan düşme oranı ile arttığı sonucuna vardık. Bu nedenle, düşen gövde, yerçekimi ve hava direncinin eşitlendiği bir hıza hızlanır ve vücut ayrıca sabit bir hızda düşer.

Doğru, bir paraşütçü söz konusu olduğunda, durum biraz daha karmaşıktır. Paraşüt hemen açılmaz ve paraşütçü önemli ölçüde daha yüksek bir hıza hızlanır. Ve paraşüt zaten açıldığında, düşüş yerçekimi kuvveti ve hava direnci kuvveti dengelenene kadar devam eden bir yavaşlama ile başlar.

Toplam kütle m sabit hızda inen bir paraşüt kargo için v, yazabiliriz: mg - F (v) = 0; burada F (v) Hava direnci kuvveti, düşme hızının bir fonksiyonu olarak kabul edilir. F (v) şu ana kadar sadece bir şey söyleyebiliriz: tekdüze bir şekilde büyüyor. Hızın dengelenmesini sağlayan bu durumdur.

En basit durumda, F (v) = k, paraşütün düşeceği sabit hız mg / k'ye eşit olacaktır. Şimdi biraz dönüşüm yapalım. Paraşüt h yükseklikten düşsün. Daha sonra, düşmeden önce ve sonra vücudun potansiyel enerjilerindeki fark mgh = mU'ya eşit olacaktır, burada U, birim yükseklikte vücut yüksekliğinin potansiyel enerjisi veya başlangıç ​​ve son insidans noktalarındaki yerçekimi alanının potansiyel farkıdır.

Yukarıdakiler ışığında, aşağıdaki formülü elde ederiz: F (v) = mU / s. (1)

Ve şimdi elektrik akımının aktığı iletkene geri dönün. Çok sayıda yüklü parçacık iletken boyunca hareket eder, bu da atomlarla daha hızlı çarpıştıklarında daha hızlı uçarlar. Bir paraşüt inişine benzetme oldukça şeffaftır, tek fark çok fazla “paraşüt” olması ve yerçekiminde değil, elektrik alanında hareket etmeleridir. Bu koşullar göz önüne alındığında, (1) şu şekilde yeniden yazılabilir: F (v) = eU / l, (2)

e'nin parçacık yükü olduğu durumda, U iletkenin uçlarındaki elektriksel potansiyel farkıdır, l iletkenin uzunluğudur.Akım gücü açıkça I = neS'ye eşittir, burada n birim hacim başına yüklü parçacık sayısıdır, S iletkenin kesit alanıdır, parçacık hızıdır (basitlik için tüm yüklü parçacıkların aynı olduğunu varsayarız).

I (U) bağımlılığını elde etmek için, F () bağımlılığını açıkça bilmeniz gerekir. En basit seçenek (F = k) hemen Ohm yasasını verir (I ~ U):

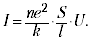
Değer iletkenlik olarak adlandırılır ve karşılık olarak direnç denir. Yasayı keşfeden şeref, direniş genellikle ohm olarak ifade edilir.

Değer (ne2 / k) spesifik iletkenlik olarak adlandırılır ve ters değeri spesifik direnç olarak adlandırılır. Bu değerler, iletkenin oluştuğu malzemeyi karakterize eder. İletkenliğin birim hacim (n) başına yüklü parçacık sayısıyla orantılı olması önemlidir. Metallerde ve elektrolit çözeltilerinde bu sayı büyüktür, ancak dielektriklerde küçüktür. Birim gaz hacmi başına yüklü parçacık sayısı uygulanan alana bağlı olabilir (yani, U'nun bir fonksiyonudur); bu nedenle Ohm yasası gazlar için geçerli değildir.

Ohm yasasını çıkarırken açık olmayan bir varsayım yaptık. Yüklü bir parçacığın hareketini engelleyen kuvvetin hızı ile orantılı olduğunu kabul ettik. Tabii ki, bir şekilde bu fikri haklı çıkarmaya çalışabiliriz, ancak deneysel doğrulama çok daha ikna edici görünüyor.

Bu varsayımın deneysel bir doğrulaması, açıkça Ohm yasasının kendisinin bir doğrulamasıdır, yani. U ve I orantılılığı. Bunun yapılması zor görünmüyor: bir voltmetre ve bir ampermetre var! Ne yazık ki, her şey o kadar basit değil. Öğrencilerimize, tıpkı bir ampermetre gibi bir voltmetrenin voltaj değil, akım gücünü ölçtüğünü açıklamalıyız. Ve voltmetrenin ölçeğine volt koyma hakkımız var, çünkü başlangıçta kontrol etmek istediğimiz Ohm yasasını biliyoruz. Başka yaklaşımlara ihtiyaç var.

Örneğin, aşağıdaki fikri kullanabilirsiniz. N pili seri olarak bağlarız ve bu durumda voltajın n kat arttığını varsayarız. Ohm yasası doğruysa, o zaman mevcut güç n kat artacaktır, çünkü n / I (n) oranı n'ye bağlı olmayacaktır. Bu varsayım tecrübe ile doğrulanır. Doğru, pillerin iç direnci de vardır, bu yüzden n / I (n) değeri artan n ile yavaş büyür, ancak bunun düzeltilmesi zor değildir. (G.Ohm'un kendisi, öğrencilerin G.Ya. Myakishev ve diğerlerinin ders kitabında okuyabileceği farklı bir şekilde stresi ölçtü.)

Şu soruyu soruyoruz: “Tau Ceti'nin uzak takımyıldızında” Ohm yasası değil, büyük yerel bilim adamı Akademik X yasası. X yasasına göre, mevcut güç, iletkenin uçlarındaki potansiyel farkın karesi ile orantılıdır. Parçacıkların frenleme kuvveti, Tau Ceti'deki hızlarına nasıl bağlıdır? ” Basit dönüşümlerin yardımıyla, öğrenciler gücün hızın kare kökü ile orantılı olduğu sonucuna varırlar.

Ve şimdi başka bir sürece geçelim: uçlarında farklı basınçların yaratıldığı bir borudaki suyun hareketi. Burada tamamen farklı bir durumumuz var: ayrı hareketli parçacıklar iletkenin tüm hacmi boyunca dağıtılan sabit bir malzemeye sürtünmez, ancak hareketli parçacık katmanları birbirine sürtünür. Ve bu durum tüm fiziksel muhakemeyi temelden değiştirir.

İki kuvvet, bir boruda hareket eden ayrı bir su tabakasına etki eder:

a) tabakanın uçlarındaki basınç kuvvetlerindeki fark;

b) komşu su katmanlarına karşı sürtünme kuvveti.

Katmanın sabit bir hızı belirlenirse, bu kuvvetler eşittir ve zıt yönlerde yönlendirilir.

Komşu su katmanlarına karşı sürtünme kuvveti, ancak farklı su katmanları farklı hızlarda hareket ederse hareketi yavaşlatabilir. Bir iletkende, yüklü parçacıkların hızı, iletkenin kenarında mı yoksa ortasında mı olduğuna bağlı değildir, ancak borunun ortasındaki su, borunun tam yüzeyinde, kenarlar boyunca hızlı ve yavaşça hareket eder, su hızı sıfırdır.

Mevcut gücün bir analogu su akışı olarak kabul edilebilir, yani. birim zamanda borudan akan su miktarı. Farklı katmanlardaki suyun hızı aynı olmadığından, akış hızını hesaplamak o kadar basit değildir.Elektrik potansiyelindeki farkın bir analogu, borunun uçlarındaki basınç farkıdır.

Akıma sahip bir iletkende olduğu gibi, uçlarda basınç farkı ile akış hızı arasında su bulunan boruda doğrudan bir orantısallık gözlenir. Ancak orantılılık katsayısı tamamen farklıdır. İlk olarak, su akış hızı sadece borunun enine kesit alanına değil, aynı zamanda şekline de bağlıdır. Boru silindirik ise, akış hızı enine kesit alanı ile değil, karesiyle (yani dördüncü dereceye kadar yarıçapla) doğru orantılıdır. Bu bağımlılığa Poiseuille yasası denir.

9. sınıfta incelenen anatomi, fizyoloji ve hijyen seyrini hatırlama zamanı. İnsan vücudunun paralel bağlı çok sayıda damarları vardır. Bu gemilerden birinin genişlediğini ve yarıçapının biraz arttığını, sadece iki kez olduğunu varsayalım. Damarın uçlarında aynı basınçla kaç kez, içinden geçen kan miktarı artacaktır? Enine kesit alanı yarıçapın karesiyle orantılıdır ve enine kesit alanının karesi dördüncü derece yarıçapı ile orantılıdır. Bu nedenle, yarıçap iki katına çıktığında, kan akışı 16 (!) Kat artar. Organlar arasında kanı yeniden dağıtmak için çok etkili bir mekanizma oluşturmamızı sağlayan Poiseuille yasasının gücü böyledir. Elektronlar kan damarlarından akmasaydı, ancak akışları sadece dört kat artardı.

Yukarıda açıklanan konunun açıklaması geleneksel konudan farklıdır. İlk olarak, konuyla ilgili olarak, mevcut saat sıkıntısı ile doğa bilimleri için kabul edilemez bir lüks olarak kabul edilebilecek üç ders harcanmaktadır. Bununla birlikte, bu, hukukun fiziksel anlamını oldukça basit ve popüler bir şekilde ortaya koymanın ve öğrencileri çeşitli fiziksel süreçleri analiz etmek için kullanabilecekleri bir metodolojiyle donatmanın mümkün olduğu gerçeğiyle doğrulanmaktadır: havadaki bir cismin düşmesi, bir borunun içindeki bir sıvının hareketi, yüklü parçacıkların bir iletken boyunca hareketi ve daha sonra elektrik akımının vakumdan ve gazlardan geçişinin analizinde.

Bu yaklaşıma disiplinlerarası entegrasyon denir. Onun yardımıyla, öğrencilere uzak, ilk bakışta fizik bölümlerindeki ortak özellikleri gösterdik, fiziğin birbiriyle bağlantılı olmayan "fiziksel yasaların" bir "demeti değil, ince bir yapı olduğunu gösterdik. Aynı şey elbette diğer bilimsel disiplinler için de geçerlidir. Ve öyle görünüyor ki, eğitim saatlerinin mantıksız bir kaybı tamamen sonuç veriyor.

Ayrıca okuyun:Multimetre nasıl kullanılır