kategoriler: Öne Çıkan Makaleler » Pratik Elektronik
Görüntülenme sayısı: 32001
Makaleye yorum: 2
Elektronik devrelerde kondansatörler
Önceki makalelerde kısaca AC devrelerindeki kapasitörlerin çalışması, kapasitörlerin AC akımını nasıl ve neden geçtiği hakkında konuştuk (bkz. AC Kondansatörler). Bu durumda, kapasitörler ısınmaz, güç onlara tahsis edilmez: sinüzoidin bir yarım dalgasında, kapasitör şarj olur ve diğerinde, depolanan enerjiyi mevcut kaynağa geri aktarırken doğal olarak boşalır.
Bu akım geçirme yöntemi, kapasitöre serbest direnç demenizi sağlar ve bu nedenle prize bağlı kapasitör karşı dönüş yapmaz. Ve tüm bunlar, kapasitördeki akımın, uygulanan voltajın tam olarak 1 / 4'ünden ileride olmasıdır.
Ancak bu aşama ilerlemesi sadece sayacı “kandırmayı” mümkün kılmakla kalmaz, aynı zamanda sinüzoidal ve dikdörtgen sinyal jeneratörleri, zaman gecikmeleri ve çeşitli frekans filtreleri gibi çeşitli devreler oluşturmayı da mümkün kılar.
Bu hikaye sürecinde, bazen daha önce söylenmiş olanları hatırlamak, tabiri caizse özetlemek gerekir. Bu, basit bir formülü hatırlamak için önceki makalelere dönmemeye veya basitçe "nedir?"
Kapasitörlerin paralel ve seri bağlantısı
Kapasitörlerin paralel bağlantısı ile toplam kapasite, kapasitelerin aritmetik toplamıdır. Doğal olarak, bu dahil etme ile, toplam kapasitans en büyük kapasitörün kapasitesinden daha büyük olacaktır. Ctotal = C1 + C2 + C3 + ... + Cn.
Seri bağlantı durumunda, toplam kapasite en küçük kapasiteden daha azdır.
1 / Ctotal = 1 / C1 + 1 / C2 + 1 / C3 + ... + 1 / Cn.
İki özdeş kapasitör seri olarak bağlandığında, toplam kapasitans bir kapasitenin yarısına eşit olacaktır: örneğin, her biri 1 μF'lik iki kapasitör bağlandığında, toplam kapasite 0,5 μF olacaktır.
Kapasitans Xc
Burada, dirençleri bağlarken olduğu gibi her şey tam tersidir: bir seri bağlantı toplam kapasitansı azaltırken, paralel olanı arttırır. Kapasitörlerde bir artış Xc kapasitansında bir azalmaya yol açtığından, kapasitörleri bağlarken bu durum unutulmamalıdır.
Xc = 1/2 * π * f * C
Matematik açısından, bu oldukça doğaldır, çünkü C kapasitesi kesirin paydasındadır. Bu arada, f frekansı aynı yerdedir, bu nedenle frekanstaki bir artış da Xc kapasitansında bir azalmaya yol açar. Bunun fiziksel anlamı, aynı kapasitör yoluyla yüksek frekansların geçmesinin daha iyi, daha engelsiz olmasıdır. Bu, düşük geçişli ve yüksek geçişli filtreler söz konusu olduğunda biraz sonra tartışılacaktır.
1 μF kapasiteye sahip bir kapasitör alırsak, 60 Hz frekans için Xc değeri 2653 Ohm olur ve 400 Hz frekans için aynı kapasitör Xc sadece 398 Ohm olur. İsteyenler bu sonuçları π = 3.14, hertz cinsinden frekans ve farads cinsinden kapasitans yerine formülle kontrol edebilirler. Sonra sonuç ohm olarak olacaktır. Her şey SI sistemine uygun olmalıdır!
Ancak kapasitörler sadece serbest sönümleme sönümleme dirençleri olarak veya doğrultucu filtrelerde kullanılmaz. Katılımları olmadan, düşük ve yüksek frekans jeneratörleri için devreler, çeşitli dalga formu dönüştürücüler, farklılaştırıcı ve entegre devreler, amplifikatörler ve diğer şemalar.
Daha sonra, kapasitörlerin çalışması gereken çeşitli elektrik sinyalleri dikkate alınacaktır. Her şeyden önce, bunlar ile gözlem için uygun periyodik sinyallerdir osiloskop.
Salınımların süresi ve sıklığı
Periyodik salınım bu nedenle, durmadan aynı formu, örneğin bir sinüzoidal salınımı tekrarlayan periyodik olarak adlandırılır. Bu tam salınımın süresi kesin olarak T periyodu olarak adlandırılır ve saniye, milisaniye, mikrosaniye olarak ölçülür.Modern elektronik bile nanosaniye (saniyenin milyarda biri) ile ilgilenir.
Saniyedeki periyot sayısına, salınımların frekansı f (ne sıklıkta) denir ve hertz cinsinden ifade edilir. 1Hz, bir salınımın, bir tam periyodun 1 saniyede gerçekleştirilme frekansıdır. Periyot ve frekans oranı, basit formül T = 1 / f ile ifade edilir.
Buna göre, salınım periyodunu bilmek, f = 1 / T frekansını hesaplamak çok basittir.
Bir osiloskop ile ölçülürken frekans bu şekilde hesaplanır: bir periyottaki hücre sayısı, bir hücrenin süresi ile çarpılır ve periyot, örneğin mikrosaniye olarak elde edilir. Sıklığı bulmak için son formülü kullandılar.
sıradan elektronik osiloskop Araştırmaya uygun bir hareketsiz görüntü elde etmek için sadece tarama frekansı ile senkronize edilebilen periyodik sinyalleri gözlemlemenizi sağlar. Bir müzik programına osiloskop girişine bir sinyal gönderirseniz, görüntüyü hiçbir şey için durduramazsınız. Bu sinyalleri gözlemlemek için depolama osiloskopları kullanılır.
Bir süre milisaniye cinsinden ölçüldüğünde, frekans kilohertz cinsinden elde edilir, mikrosaniye cinsinden ölçülen bir süre için, frekans zaten megahertz cinsinden ifade edilir. SI sisteminin gereksinimlerine uymuyorsanız: saniye cinsinden süre, hertz cinsinden frekans.
Sinüzoidal olmayan titreşimler
Daha önce de belirtildiği gibi, sinüs dalgası periyodik eğrinin çalışması ve pratik kullanımı için en yaygın ve uygundur. Endüstriyel koşullarda, örneğin hidroelektrik santrallerinde elektrik jeneratörleri kullanılarak elde edilir. Elektronik cihazlarda, en çeşitli şekillerin titreşimleri kullanılır.
Temel olarak, bunlar üç formdur: Şekil 1'de gösterildiği gibi sinüzoidal, dikdörtgen ve üçgen, hem akım hem de voltaj böyle bir şekle sahip olabilir, bu nedenle şekil sadece zaman eksenini gösterir, sıra ekseni bir ad olmadan bırakılır.
Bu salınımlar özel elektronik devreler tarafından üretilir. Dikdörtgen ve üçgen sinyallere genellikle darbeli denir. Bununla birlikte, sinyal dönüşümü yapan birçok elektronik devre vardır: örneğin, bir dikdörtgen, bir sinüzoidden bir üçgen yapılabilir.
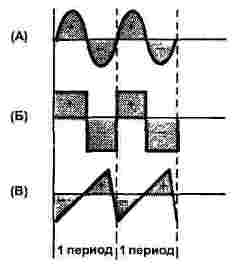
Resim 1
Her üç sinyal için, şekil iki periyot gösterir, tüm sinyaller aynı frekansa sahiptir.
Sinüzoidal olmayan sinyallerin spektrumu
Herhangi bir elektrik sinyali, zamanın bir noktasında genliğin bir ölçümü olarak temsil edilebilir. Bu örneklerin frekansına örnekleme frekansı denir ve ölçülen sinyalin üst frekansından en az iki kat daha fazladır. Daha sonra bu örneklerden orijinal sinyali geri yükleyebilirsiniz. Bu yöntem, örneğin dijital ses kaydında kullanılır. Bu yönteme zaman analizi de denir.
Başka bir yöntem, herhangi bir sinyalin, hatta dikdörtgen bir sinyalin, farklı frekans ve fazlara sahip sinüzoidlerin cebirsel toplamı olarak temsil edilebileceğini varsayar. Bu yönteme frekans analizi denir. Ancak, “farklı frekanslarda” söylenen şey tamamen doğru değildir: kurucu sinüzoidlere harmonik denir ve frekansları belirli yasalara uyar.
Frekansı kare dalganın frekansına eşit olan bir sinüs dalgasına temel veya ilk harmonik denir. Hatta harmonikler bile temel frekansın çift sayı ve tek harmonikler tek sayı ile çarpılmasıyla elde edilir.
Böylece, ilk harmonik 1000 Hz'lik bir frekansa sahipse, ikincisi 2000 Hz, dördüncü 4000 Hz'dir. Tek harmoniklerin 3000Hz, 5000Hz frekansları olacaktır. Ayrıca, her harmonik genlikten ana harften daha küçüktür: harmonik ne kadar yüksekse, genlik o kadar küçük olur.
Müzikte harmoniklere tonlama denir. Ses tınılarını oluşturan, kemanı piyanodan ve gitarı saksafondan ayırt etmeyi mümkün kılan onlardır. Erkek ve kadın sesini karıştırmaya veya Petrov'u Ivanov'dan ayırmaya izin vermezler. Ve sadece sinüzoidin kendisi artık herhangi bir sinyalden ayrıştırılamaz veya birleştirilemez.
Şekil 2, dikdörtgen bir darbenin yapısını göstermektedir.
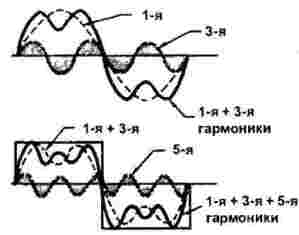
Resim 2
Birinci ve üçüncü harmonikler şeklin üst kısmında gösterilmiştir. Üçüncü geçişin ilk harmonik üç periyodunun bir döneminde görülmesi kolaydır. Bu durumda, üçüncü harmoniğin genliği birincinin üçte biridir. Birinci ve üçüncü harmoniklerin toplamı da burada gösterilmektedir.
Aşağıda, 1 ve 3 harmoniklerin toplamı ile birlikte, başka bir 5 harmonik gösterilmektedir: dikdörtgen bir sinyal periyodu için tam olarak beş periyot yapmayı başarır. Bu durumda, genliği daha küçük, daha kesin olarak, ana (ilk) olanın tam olarak 1 / 5'i kadardır. Ancak, her şeyin beşinci harmonikte sona erdiğini düşünmemeliyiz: Şekilde gösterilemez, aslında çok daha fazlası vardır.
Şekil 3'te gösterilen testere dişi ve üçgen sinyallerin oluşumu biraz daha karmaşıktır.Bir önceki durumda sadece tek harmonikler yer aldıysa, harmonikler bile devreye girer.
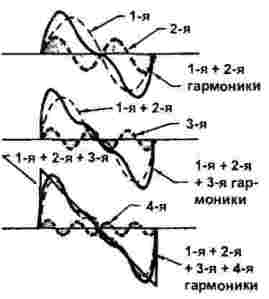
Şekil 3.
Böylece, birçok harmoniğin yardımıyla herhangi bir şekle sahip bir sinyalin sentezlendiğini ve harmoniklerin sayısı ve tipinin, Şekil 2 ve 3'te gösterildiği gibi dalga formuna bağlı olduğunu söyleyebiliriz.
Elektronik ekipmanı onarırken ve kurarken, elektrik sinyallerini incelemek için bir osiloskop kullanılır. Periyodik sinyallerin formunu, genliklerini düşünmenizi, tekrar periyodunu ölçmenizi sağlar. Ancak Şekil 2 ve 3'te gösterilen harmonikler görülemez.
Örneğin, bir elektro gitarı bir osiloskopa bağlasanız bile, bir ipi çekin, ekranda bir sinüzoid görünür, ilk harmoniktir. Bu durumda, herhangi bir imadan söz edilemez. Aynı sinüzoid, borunun içine üfler veya mikrofonun önünde flüt yaparsanız ortaya çıkar.
Dikdörtgen impulslar nasıl elde edilir
Elektrik sinyallerini öğrendikten sonra, makalenin başladığı kapasitörleri hatırlamamız gerekir. Her şeyden önce, klasik elektronik devrelerden birini tanımanız gerekir - multivibratör, (Şekil 4) dikdörtgen darbeler üreten kişidir. Devre o kadar klasik ki herhangi bir ayar veya ayar gerektirmeden hemen çalışmaya başlar.
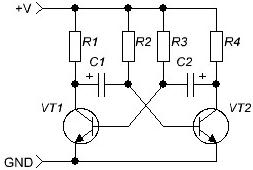
Resim 4
Multivibratör pozitif geri besleme ile kaplanmış iki aşamalı bir amplifikatördür. Kolektör yük dirençleri R1 = R4, taban dirençleri R2 = R3 ve kapasitörler C1 = C2 eşitse, multivibratör simetrik olarak adlandırılır ve kıvrımlı tipte kare dalga darbeleri üretir - darbe süresi duraklama süresine eşittir.
Bu darbelerin görev döngüsü (dönemin darbe süresine oranı) ikiye eşittir. İngilizce şemalarında, her şey tam tersi: buna görev döngüsü diyorlar. Nabız süresinin art arda dönme süresine oranı olarak hesaplanır ve yüzde olarak ifade edilir. Böylece, kıvrımlı için görev döngüsü% 50'dir.
Bilgisayar doğru mu?
Multivibratör adı, Hollandalı fizikçi van der Pol tarafından önerildi, çünkü dikdörtgen bir sinyalin spektrumu birçok harmonik içeriyor. Ses frekansında bile çalışan bir multivibratörün yanına orta dalga aralığında çalışan bir radyo alıcısı yerleştirebiliyorsanız bunu doğrulayabilirsiniz: hoparlörden ulumalar gelecek. Bu, ses frekansına ek olarak, multivibratörün de yüksek frekanslı salınımlar yaydığını gösterir.
Üretim frekansını belirlemek için f = 700 / (C1 * R2) formülünü kullanabilirsiniz.
Formülün bu formu ile, kapasitörün mikrofaradlardaki kapasitesi (μF), kilo-ohm (KΩ) cinsinden direnç, hertz (Hz) ile sonuçlanır. Böylece, frekans C1 * R2 devresinin zaman sabiti tarafından belirlenir; toplayıcı yükleri frekansı etkilemez. C1 = 0.02 μF, R2 = 39 KΩ alırsak, f = 700 / (0.02 * 39) = 897.4 Hz alırız.
Bilgisayar çağında multivibratör ve mikrokontrolörler Bu şemaya göre, neredeyse hiç kullanılmaz, ancak çeşitli deneyler için uygun olabilir. Her şeyden önce, bilgisayar kullanarak. Multisim programında monte edilen multivibratör devresi böyle görünür. Osiloskopun bağlantısı da burada gösterilmiştir.
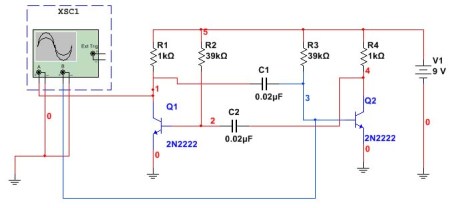
Resim 5
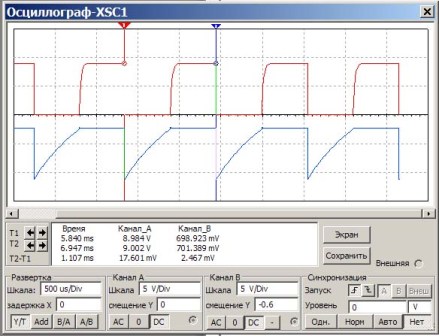
Bu devrede, önceki örnekteki gibi kapasitörler ve dirençler monte edilir. Görev, aynı frekansın elde edilip edilmeyeceğini formüle göre hesaplamayı kontrol etmektir. Bunu yapmak için, darbelerin süresini ölçün ve daha sonra frekansları yeniden hesaplayın. Multisim osiloskopun sonucu Şekil 6'da gösterilmektedir.
Resim 6
Şekil 6'ya ilişkin bazı açıklamalar.
Osiloskop ekranında kırmızı puls, transistör toplayıcısındaki darbeleri ve bazlardaki maviyi gösterir. Büyük beyaz bir pencerede ekranın altında, sayılar ölçüm sonuçlarını gösterir. "Zaman" sütunuyla ilgileniyoruz. Zaman T1 ve T2 göstergeleri ile ölçülür (ekranın üstündeki kırmızı ve mavi üçgenler).
Böylece, darbe tekrarlama süresi T2-T1 = 1.107 ms oldukça doğru bir şekilde gösterilmektedir. Sadece f = 1 / T = 1 / 1.107 * 1000 = 903Hz frekansını hesaplamak için kalır.
Sonuç, biraz daha yüksek verilen formüle göre hesaplamadaki ile hemen hemen aynıdır.
Kondansatörler sadece ayrı olarak kullanılabilir: dirençlerle birlikte, sadece çeşitli filtreler oluşturmanıza veya faz kaydırma devreleri oluşturmanıza izin verir. Ancak bu bir sonraki makalede ele alınacaktır.
Makalenin devamı: Elektronik devrelerde kondansatörler. Bölüm 2
Boris Aladyshkin
Ayrıca bkz. electro-tr.tomathouse.com
: